In the past few years, tech giants like Google, Microsoft, and others have put their heft into quantum computing. Their efforts make sense.  Quantum computing holds greater promise for large computations and these companies have some of the largest stores of data in human history.  Venture capital and investor interest in quantum computing has also surged as a range of companies show enthusiasm for integrating quantum into their business processes. BMW, for one, is exploring how quantum might yield improvements across a range of automotive activities, from battery chemistry to sales. What’s more, a burgeoning ecosystem of “quantum computing as a service” providers and partners have sprung up to keep partners across industries up to date on the latest advances and possibilities. 

Quantum Economic Advantage: A New Practical Framework

With all this activity, it’s tempting to think that quantum computing will be the successor to traditional computing, and that all problems will be solved with quantum computers in the future. But while there is the potential for some problems to be solved dramatically faster, for many others quantum computing will be a poor fit and classical computers will remain the better choice. So, how’s a firm to know the difference? 

Whether quantum computers will outperform classical ones can be understood as a race, where winning depends on hardware speed and algorithms. The role of each can be understood by analogy to a ship: hardware speed is the speed of the ship and the algorithm is the route the ship takes. Classical computers are much faster than quantum computers, but sometimes quantum computers have dramatically better algorithms. So, in our analogy, classical computers would always be better in open water, where both have access to the best route (algorithm).  Conversely, there will be special cases, say going from one side of Panama to the other, where having access to a better route (the Panama Canal) will make an enormous difference.  These special cases arise because some algorithms are only available to quantum computers (e.g., Shor’s algorithm in cryptography) and these can offer dramatically better routes.

This provides our first insight – if quantum computers don’t have access to a better algorithm, then classical computers will easily outpace them and classical computing will continue to be used for this problem in the future.  But what about the cases when there are better quantum algorithms, or could be in the future?  Then, it isn’t guaranteed that quantum would have an advantage – we need a framework to understand when it will and when it won’t. 

To this end, we propose a straightforward framework that can be used to think about quantum computing from a practical perspective – which we call “Quantum Economic Advantage.” Those who follow quantum computing are likely familiar with the related term “Quantum Advantage,” which occurs when quantum computers exist that can outperform any classical computer for some problem. While very useful for asking what can only be done by quantum computers, it doesn’t work well for near-term decision-making as we start facing problems that both classical and quantum computers can solve.  Our framework provides a remedy. Quantum Economic Advantage occurs for a problem when quantum computers exist that can outperform any comparably expensive classical computer for that problem.

In simple terms, two things are needed to get quantum economic advantage: (i) feasibility: the quantum computer must be powerful enough to solve the problem, and a (ii) net algorithmic advantage: the benefit of the better quantum algorithm must be sufficiently large to overcome the speed advantage of comparably expensive classical computers.  

Feasibility: Building a Sea-worthy Ship 

Questions of hardware have dominated the quantum computing discourse for many years, focusing particularly on the qubit, the fundamental quantum computing unit. Just as it’s not feasible to play the most-recent 64-bit Mario Kart game on an 8-bit Nintendo, you can’t solve a quantum problem with qubits you don’t have. For a nascent technology like quantum, it makes sense to ask when its capabilities will be sufficient to tackle a particular problem. This is “quantum feasibility.” 

For a quantum computer, it is important not only that there are enough qubits to process a problem, but that these qubits can maintain their state and their entanglement, the delicate quantum property that allows quantum computers to do calculations not possible on classical ones. Quantum feasibility is achieved when a quantum computer, running codes to minimize the accumulation of such errors, has enough viable qubits to solve a given problem. 

Even once it is possible to solve a problem on a quantum computer, it is not at all obvious that you would want to use one to solve your problem.  That’s because, in general, classical computers are dramatically faster – in our analogy, classical computers are speedboats and quantum computers are slow steamers.  So why would you ever want to use a quantum computer?  Because sometimes they have dramatically shorter routes available to them for doing a calculation.

Algorithmic Advantage: Does your Ship have a Shortcut?

Quantum computers are slower than classical computers.  Much slower. In the time it would take a quantum computer to do one step in a calculation, a classical computer could do roughly 1,000,000 of them. Faced with such a dramatic speed disadvantage, one might imagine that quantum computers would lose any race. But, as with the shortened route offered by the Panama Canal, sometimes there can also be enormous advantages to better algorithms. If this difference in route is sufficiently consequential, then the quantum steamer can outpace the classical speedboat.

Right now, we only know a small number of problems where the shortcut provided by quantum algorithms makes a big difference. One is factoring, which is used in cryptography.  Factoring a 2048-bit number classically would take approximately 1016 CPU-years (equivalent to a million computers running for the age of the universe). In contrast, Shor’s quantum algorithm could theoretically solve it in days. So factoring is a case where there will a net algorithmic advantage for this size of problem.  The challenge is feasibility.  Shor’s algorithm would require about 107 to 108 logical qubits to factor a 2048-bit number, far more than current quantum computers (or any near-term ones) will have.  So, our framework says that Shor’s algorithm could provide quantum economic advantage for this problem, but only in many years, once quantum hardware gets much better.

Enormous effort is being expended to discover new quantum algorithms. But even before these new algorithms arrive, careful analysis can reveal where quantum has the biggest potential to provide Quantum Economic Advantage.  In what follows, we provide the recipe for doing these calculations and provide a few examples of how to do it.

For firms trying to understand where quantum will matter for them, the key is to lay out the race that quantum and classical computers will be running for the problem that they care about.  Quantum will win if its algorithmic improvement outpaces the 1,000,000x advantage that classical computers have.  Fortunately, when computer scientists invent new algorithms, they provide the information needed to calculate this when they describe how many steps the algorithms require.  This is usually expressed as a function of N, the size of the problem.  For example, the best classical algorithm for searching text scales as O(N), meaning that as the problem gets bigger, the number of steps in the calculation grows linearly with N.  In contrast, the best quantum algorithm for this (Grover’s) scales proportionally to  so the steps grow as the square-root of the problem size.  Without getting too into the technical details, this means that if the text search was done on a sequence with 100 letters (N=100) then the classical algorithm would require 10x times more steps ().  Since that is not enough to counter-balance the 1,000,000x speed difference, classical computers would still be faster for this task.  As problem sizes get bigger, this trade-off changes and quantum becomes faster, as shown in Figure 1.

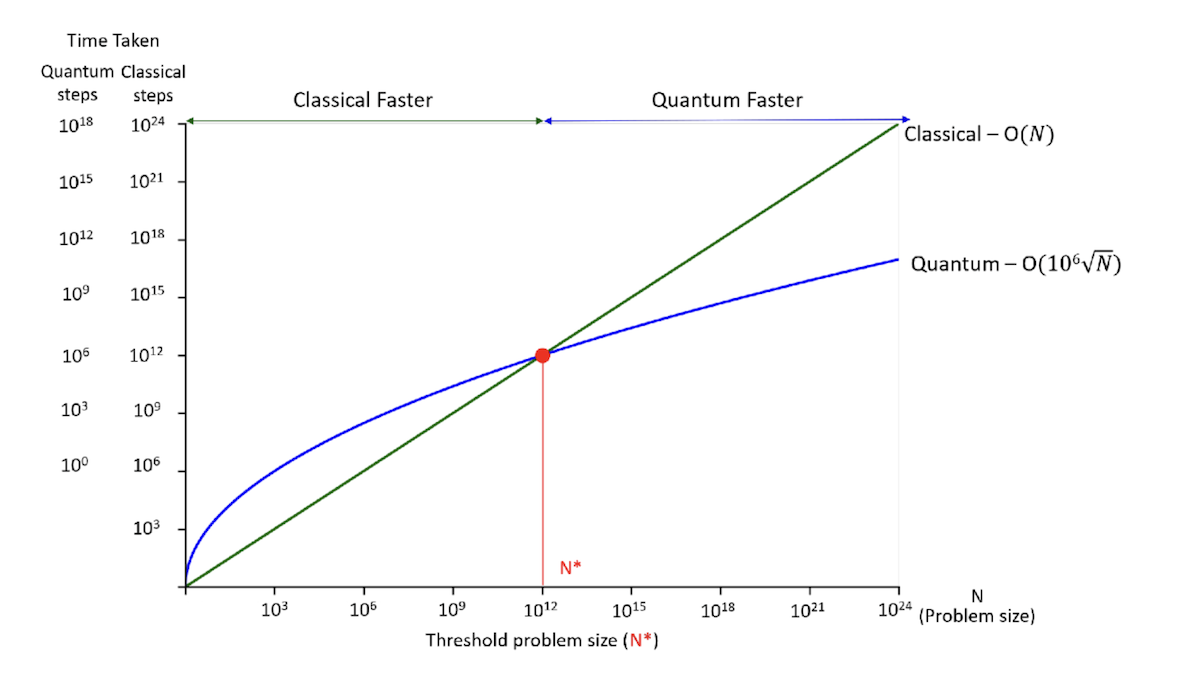
Figure 1: Comparing classical and quantum algorithms for text search

This graph highlights a particularly important property: the bigger the problem being tackled, the larger is the benefit from a better quantum algorithm. This graph also shows that for all problems where there is a better quantum algorithm, there will also be a threshold, N*, where the problem is large enough that the algorithm benefit eclipses the speed difference.  For Grover’s algorithm, this cutoff happens at N=1 trillion (i.e.,1012), so Grover’s algorithm would only be advantageous for problems larger than this.  This result also means that quantum computers will need to feasibly handle problems of size 1012 before they can be competitive. Since Grover’s algorithm needs log2(N) qubits, or about 40 (≈ log2(1012)) logical qubits to do this. After taking into account error correction issues, this would require roughly a 40,000-qubit machine.  This is vastly more qubits than today’s quantum computers, which only have hundreds.  Nevertheless, if quantum hardware providers continue improving their systems exponentially (and can keep qubit quality up), then we would have this number of qubits by 2031  And, indeed, this would be the first moment when we would expect Grover’s algorithm to have a real advantage. Of course, this could also happen more slowly, if quantum computer roadmaps are too optimistic, or if other needed technical developments (e.g., Quantum RAM) are not developed.

While our method cannot overcome these technical uncertainties, it nevertheless provides important information for prospective users of quantum computing because the analysis above is the first moment when quantum computers could be better for this type of problem. Other problems, either larger or smaller, would take even longer to get quantum economic advantage because either the systems would need to be more powerful to handle them (for larger problems) or because additional improvement would be needed in quantum computers to outpace classical computers (for smaller problems).  In either case, firms deciding whether a particular quantum would be useful for them, would know that they could postpone serious consideration until nearer to the year of first quantum economic advantage for their problem.

What is being done today?

Companies in various industries including pharmaceutical, banking, and insurance are already exploring how quantum algorithms might give them a competitive advantage. The following examples illustrate the potential of the Quantum Economic Advantage framework for making benefits and timelines concrete: 

1. Risk Analysis. Analyzing financial risk is essential for pricing securities, managing portfolio investments, and deciding which parts of a portfolio should be reinsured. Classically, risk calculation is done using Monte Carlo simulations where increasing precision requires increasing the amount of computational steps by .  So, for example, doubling the precision would require four times as much computation.

Quantum Monte Carlo algorithms are better, requiring computation proportional to .  Based on the quantum economic advantage framework and relative speed difference of 106x between classical and quantum, we would expect the precision provided by quantum to outpace classical machines when  - that is, when N > 106.  So, Quantum Monte Carlo will only be useful for those doing risk analysis with more than 106 Monte Carlo simulations.  

We can also ask when we would expect this to be possible. In this case, the number of qubits required needs to include both the cost of increased precision (N=106 would require log2(106) ≈ 20 logical qubits), plus an additional number of logical qubits needed to encode the risk value itself. Previous research put this latter number at ~8,000 (cite).

So, once we account for error correction, we should expect these systems to arrive in 2043.

2. Drug Discovery. Computational chemistry is central to advancing drug discovery, because it predicts which drugs will bind to receptors in the human body. However, simulating a chemical system on a classical computer is hard.  The number of steps that a classical computer needs to perform chemical simulation grows exponentially with the number of electrons around atoms or molecules. Therefore, as molecules get bigger, the number of computations grows quickly, roughly equal to 10N (where N is the number of electrons).  A recent research paper suggests that Quantum computers can solve this problem much more efficiently using a quantum phase estimation algorithm, with the number of operations only growing like 6.3N6.5 steps. If we again apply our 1,000,000x speed penalty, we can solve for how many electrons a molecule must have before it becomes better to solve on a quantum computer, and when we would expect this problem to be feasible on a real quantum computer.  We find that N*=26, so when N>26, the quantum algorithm solves the problem faster than an equivalently expensive classical computer.  Using this quantum algorithm with N=26 requires 1,400 logical qubits, or 1,400,000 physical qubits, meaning that this technique should be useful by 2039 according to quantum computing roadmaps.

Your Department of Quantum Computing 

Quantum computers won’t be better at everything.  They’ll only be better at problems that can be solved with particular algorithms and where the problem size is big enough for the algorithmic benefit to be large. Therefore, a key function of any firm’s department of Quantum Computing must be to understand how big the firm’s problem sizes are and whether better quantum algorithms exist for these problems.

This article provides the framework that will help firms understand if the computational problems they care about will have Quantum Economic Advantage and how long firms will need to wait to get quantum computing hardware with enough viable qubits to handle it. Even better, this framework can be used for scenario planning. See Figure 2.  Imagine that either a better quantum algorithm has yet to be discovered for a problem, or perhaps the firm just doesn’t have the expertise to check.  The framework above could still be used, just with hypothetical values for how good the quantum algorithm is.  This will allow “what-if” analyses, for example if a quantum algorithm like X is discovered, the company would need to be ready to use it in Y years, whereas if quantum algorithm W is discovered instead, that horizon would be X years.  Thus, this analysis can still inform firms in uncertain situations about when to invest in understanding quantum.

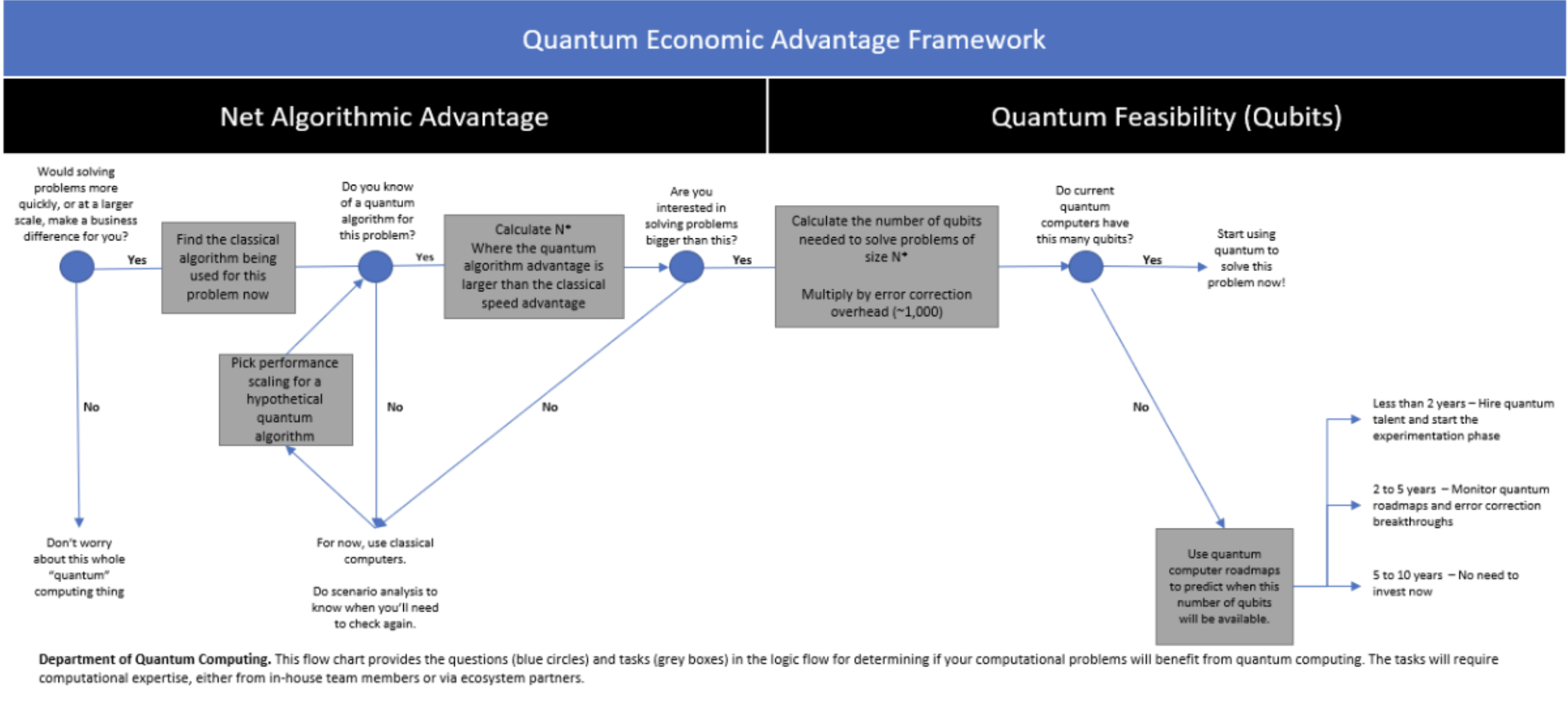
Figure 2. Quantum Economic Advantage Framework

For most firms, it will still be too early to have a full department of quantum computing.  These firms should instead use internal or external expertise to develop quantum readiness dashboard.  This dashboard would show where the firm has the most potential for quantum improvement and what triggers (e.g., the development of a better quantum algorithm or an improvement in quantum error correction) would transition them from pilot projects to full deployment.  By focusing on this Quantum Economic Advantage framework, that roadmap can be made concrete.